The Soft-Gamma-Agreement : an alternate measure to gamma

To complete the gamma-agreement, we have added an option called “soft” gamma. It is a small tweak to the measure created with the goal of doing exactly what gamma does, except it reduces the disagreement caused by splits in annotations.

The idea behind this concept is to make use of the gamma agreement with machine learning models, since most of the existing ones are prone to produce of lot more splitted annotations than human annotators.

How to use soft-gamma

The soft-gamma measure, for the user at least, works exactly like gamma :

continuum = pa.Continuum.from_csv("tests/data/AlexPaulSuzan.csv")
dissim = pa.CombinedCategoricalDissimilarity(delta_empty=1,
                                             alpha=0.75,
                                             beta=0.25)
gamma_results = continuum.compute_gamma(dissim, soft=True)

print(f"gamma = {gamma_results.gamma}")
pa.show_alignment(gamma_results.best_alignment)

The only difference will be the look of the resulting best alignment, as well as the gamma value. This new gamma can be higher than the normal gamma (it is very unlikely to be lower). The more splitted annotations the input continuum contains, the wider the differences between the two measures will be.

Here is a comparison of those two measures, with two types of errors generated by the corpus shuffling tool :

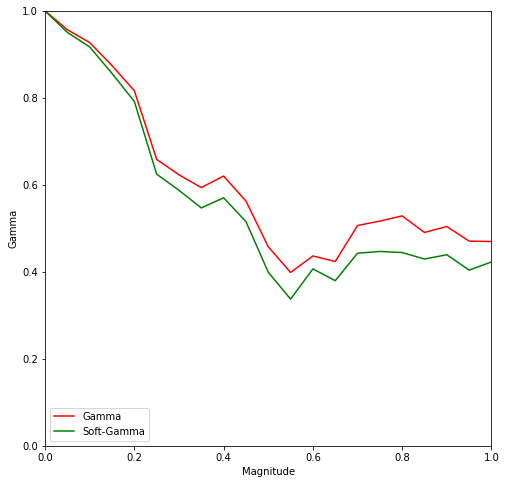
Shifted annotations, 3 annotators.

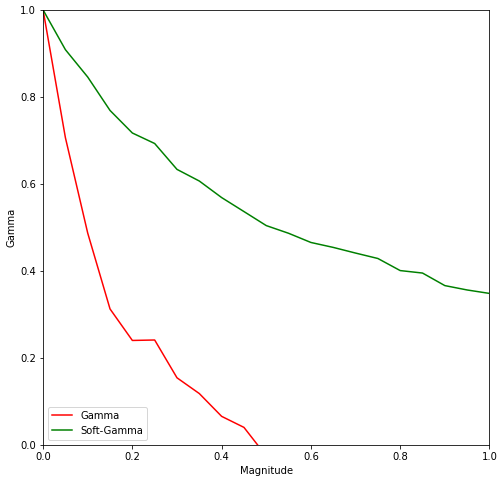
Splitted annotations, 3 annotators.

For shifts, a magnitude of \(p\) means every start and end of unit is shifted by a random value between \(0\) and \(p \times l\), where \(l\) is the duration of the unit.

For splits, a magnitude of \(p\) means that for an annotator who has annotated \(n\) segments, \(p \times n \times 2\) units are successively chosen at random to be split at a random time. A unit can be splitted more than once.

As pointed before, the gamma-agreement is very sensitive to split annotations. Soft-gamma was created with the intent of reducing the penalty of splits while keeping a similar value if none are involved.

What is soft-gamma ?

This section will explain the differences between the two measures. Beware that it requires a bit of knowledge about the gamma-agreement. You can learn more about it in the “Principles” section :

“A unitary alignment is a tuple of units, each belonging to a unique annotator. For a given continuum containing annotations from n different annotators, the tuple will have to be of length n. It represents a “match” (or the hypothesis of an agreement) between units of different annotators. A unitary alignment can contain empty units, which are “fake” (and null) annotations inserted to represent the absence of corresponding annotation for one or more annotators.”

The main difference between soft-gamma and gamma is their definition of an Alignment, which the algorithms find the best possible based on the dissimilarity measure.

for Gamma :

“An alignment is a set of unitary alignments that constitute a partition of a continuum. This means that each and every unit of each annotator from the partitioned continuum can be found in the alignment once, and only once. “

To illustrate, let’s visualize an alignment :

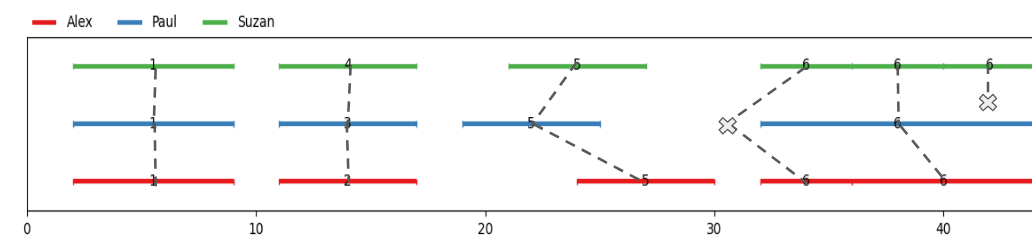
Every unit must be present exactly once, meaning splits create alignments with empty units, resulting in an additionnal disorder cost of more than \(\Delta_\emptyset \times n\) per split.

for Soft-Gamma :

“A soft-alignment is a set of unitary alignments that constitute a superset of a continuum. This means that each and every unit of each annotator from the partitioned continuum can be found in the alignment at least once.”

To illustrate, let’s visualize an alignment :

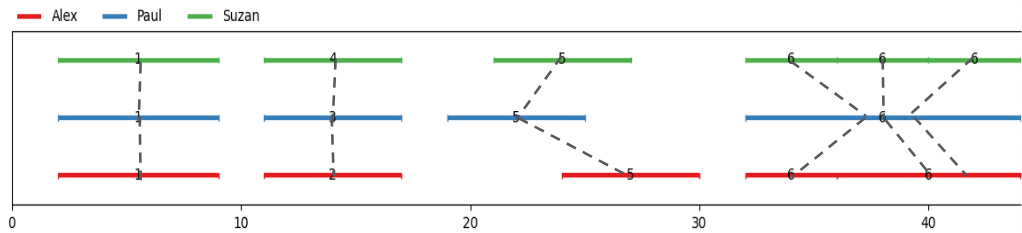
Every unit must be present at least once, meaning splits create multi-aligned units, with significantly lower cost. Thus, this alignment will be preferred as the one before.

This definition ensures empty units are added to mark up a false negative and not to complete the partition of the continuum with unitary alignments.

How does soft-gamma reduce split cost ?

The important effect of a soft-alignment is that it limits the occurence of “empty units” in the best possible alignment. With the ‘gamma’ definition of an alignment, in most cases, splits cause empty units to appear in the best alignments.

This is because with the constraint of having every unit (except empty ones) appear exactly once in the best alignment, the algorithm will naturally ‘fill the gaps’ with empty units when there’s a split : if an annotator has written down two annotations where the other has annotated only once, an empty unit will make its way into the best alignment.

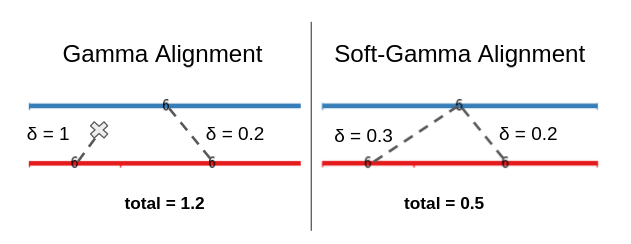
With the soft-gamma definition, the resulting cost of such a split will only be the sum of the two possible alignment, which is usally a lot lower than the cost of using the empty unit. Naturally, this depends on the nature of the dissimilarity used : one must ensure that it isn’t more advantageous to use lots of empty units.

Combining soft-gamma with gamma-cat

Combining a “soft”-alignment with the gamma-cat or gamma-k measure (which uses the best alignment determined by the algorithm) is very much possible. Simply do just as you would with the normal gamma :

continuum = pa.Continuum.from_csv("tests/data/AlexPaulSuzan.csv")
dissim = pa.CombinedCategoricalDissimilarity(delta_empty=1,
                                             alpha=0.75,
                                             beta=0.25)
gamma_results = continuum.compute_gamma(dissim, soft=True)

print(f"gamma-cat = {gamma_results.gamma_cat}")
print(f"gamma-k('7') = {gamma_results.gamma_k('7')}")

We would recomment this version of gamma-cat instead of the classical one, since the less overwhelming amount of null units seems to suit more the objective of gamma-cat, which is only determining the exactitude of categorization of a continuum, and splitting causes the appearance of null units which is equivalent to not having an unexisting category and thus categorizing wrong even when two annotations with the same category are indeed overlapping.